7. Propiedades Termodinámicas¶

En este documento se presenta el cálculo de las propiedades termodińámicas de la fugacidad, entalpía y entropía para el caso de un componente puro y una mezcla de C componentes a una presión P, temperatura T, Volumen V y número de moles N utilizando ecuaciones de estado como Soave-Kwong (SRK) [1] y Peng-Robinson (PR) [1] y las reglas de mezclado de Van Der Waals (VDW) [1] siguiendo el enfoque modular presentado por Michelsen and Mollerup [1].

Advertencia

Falta incluir las propiedades termodinámicas entalpía y entropía.

Nota

Falta incluir más modelos de ecuaciones de estado y reglas de mezclado. En el caso de RKPR falta incluir ejemplos en la documentación.

Para desarrollar el trabajo de este documento se utiliza el lenguaje de programación Python [2] y la documentación del mismo se desarrolla con la librería Sphinx 1.3.1 [3]

Nota

En este proyecto, se desarrolla de forma paralela la documentación utilizando la tecnología IPython notebook - Jupyter [4].

7.1 Implementación básica¶

De esta forma, la parte inicial del código en el lenguaje de programación Python, corresponde a la importación de la librería Numpy la cual aporta un tipo de datos denominado array que facilita la manipulación de la información para realizar cálculos con Python.

Nota

Se importa la libreria numpy con el alias np

Luego se continua con la definición de la clase Helmholtz(): y la inicialización de la misma, con la lectura de los parametros eq, w, Tc, Pc, Tr, R en el método «constructor» __init__ de la clase, señalando que el parametro self no es una palabra reservada del lenguaje Python pero es una convención ampliamente utilizada por la comunidad de usuarios y desarrolladores de código Python bajo el paradigma de programación orientada a objetos:

import numpy as np
from scipy import optimize

class Thermophysical_Properties():

    def __init__(self, eq, w, Tc, Pc, Tr, R):
        """
        eq = Ecuación de estado (SRK = 1) (PR = 2)
        w = factor acentrico
        Tc = temperatura critica del componente i
        Pc = presión critica del componente i
        Tr = temperatura reducida del componente i
        R = costante universal de los gases 0.08314472 [=] bar.l/(mol.K)
        """

        self.eq = eq
        self.w = w
        self.Tc = Tc
        self.Pc = Pc
        self.Tr = Tr
        self.R = R
        if self.eq == 1:
            # Soave-Redlich-Kwong (SRK)
            self.s1, self.s2 = 1, 2
            self.m = 0.480 + 1.574 * self.w - 0.175 * self.w ** 2
            self.ac = 0.077796070 * self.R ** 2, self.Tc ** 2 / self.Pc
            self.bc = 0.086640 * self.R * self.Tc / self.Pc
        elif self.eq == 2:
            # Peng-Robinson (PR)
            self.s1, self.s2 = 1 + 2 ** 0.5, 1 - (2 ** 0.5)
            self.m = 0.37464 + 1.54226 * self.w - 0.26992 * self.w ** 2
            self.ac = 0.45723553 * self.R ** 2 * self.Tc ** 2 / self.Pc
            self.bc = 0.077796070 * self.R * self.Tc / self.Pc
            #Martín Cismondí
            #self.ac = np.array([2.4959, 2.4959, 208.4949])
            #self.bc = np.array([0.026802, 0.056313, 0.530667])
            #self.m = np.array([0.392414, 0.603252, 1.716810])
        else:
            print ("Che boludo... Modelo no valido, intentaló de nuevo !!! ")

Relación simple del número de moles de la mezcla multicomponente

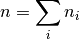
(1) $n = \sum\limits_{i} {n_i}$

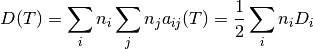
(2) $D(T) = \sum\limits_{i} {n_i \sum\limits_{j} {n_ja_{ij}(T)} = {1\over 2} \sum\limits_{i} {n_i D_i} }$

Donde 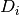$D_i$ es la derivada de 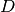$D$ con respecto al número de moles 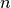$n$ de la mezcla.

a continuación se presentan las primeras derivadas parciales de la función D con respecto a las variables del sistema

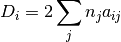
(3) $D_i = 2 \sum\limits_{j} {n_ja_{ij}}$

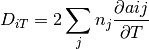
(4) $D_{iT} = 2 \sum\limits_{j} {n_j \frac{\partial aij} {\partial T}}$

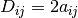
(5) $D_{ij} = 2 a_{ij}$

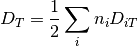
(6) $D_T = \frac{1} {2} \sum\limits_{i} {n_iD_{iT}}$

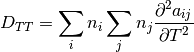
(7) $D_{TT} = \sum\limits_{i} {n_i \sum\limits_{j} {n_j} \frac{\partial^2 a_{ij}} {\partial T^2}}$

Para determinar el valor del parametro D y continuar con el algoritmo se utiliza el siguiente bloque de código en lenguaje de programación Python:

def parametro_D(self):
    if self.nC == 1:
        self.D = self.ni ** 2 * self.a_ii
        self.Di = 2 * self.ni * self.a_ii
    elif self.nC > 1:
        di = np.ones((len(self.ni), len(self.ni)))
        self.Di = np.ones((len(self.ni)))
        self.D = np.ones((len(self.ni)))
        for i in range(self.nC):
            for j in range(self.nC):
                di[i, j] = self.ni[j] * self.aij[i, j]
                self.Di[i] = 2 * np.sum(di[i, :])
        self.D = 0.5 * np.sum(ni * self.Di)

    return self.D

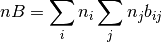
(8) $nB = \sum\limits_{i} {n_i \sum\limits_{j} {n_jb_{ij}}}$

Para el caso de un componente puro en el sistema, el parametro B (lij = 0) se calcula como:

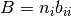
(9) $B = n_i b_{ii}$

y para el caso de una mezcla:

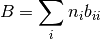
(10) $B = \sum\limits_{i} n_i b_{ii}$

Las derivadas parciales del parametro B con respecto al número de moles, se obtiene de la siguiente forma:

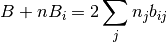
(11) $B + nB_i = 2 \sum\limits_{j} {n_jb_{ij}}$

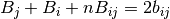
(12) $B_j + B_i + nB_{ij} = 2b_{ij}$

Resolviendo el sistema de las ecuaciones (9) y (10) se obtiene:

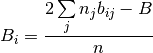
(13) $B_i = \frac{2 \sum\limits_{j} {n_jb_{ij} - B} } {n}$

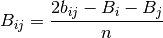
(14) $B_{ij} = \frac{2 b_{ij} - B_i - B_j} {n}$

Para determinar el valor del parametro B y continuar con el algoritmo se utiliza el siguiente bloque de código en lenguaje de programación Python:

def parametro_B(self):
    if self.nC == 1:
        self.B = self.ni * self.b_ii
    elif self.nC > 1:
        self.aux = np.zeros((len(self.ni)))
        for i in range(self.nC):
            for j in range(self.nC):
                self.aux[i] = self.aux[i] + self.ni[j] * self.bij[i, j]

        self.B = np.sum(self.ni * self.b_ii)

    return self.B

La presión P del sistema se determina por medio de la ecuación de estado que se eliga de acuerdo a las opciones inicialmente planteadas:

def presion(self):
    '''
    Con el metodo presion(), se calcula la Presión P(T, V, N) del sistema
    para una temperatura T, cantidad de moles N y un volumen V
    R = Constante universal de los gases
    nT = Número total de moles en el sistema
    Pcal = Presión calculada con la ecuación de estado
    Arv = Primera derivada parcial de la energía de Helmholz con respecto al
    volumen V, a T y N constantes
    '''
    self.gv = self.R * self.B / (self.V * (self.V - self.B))
    self.fv = - 1 / ((self.V + self.s1 * self.B) * (self.V + self.s2 * self.B))
    self.ArV = -self.nT * self.gv * self.T - self.D * self.fv
    self.Pcal = self.nT * self.R * self.T / self.V - self.ArV
    return self.Pcal

Se requiere el calculo de la primera derivadad de la presión con respecto al volumen a temperatura y número de moles constantes:

def dP_dV(self):
    self.dPdV = -self.ArV2 - self.R * self.T * self.nT / self.V ** 2
    return self.dPdV

Calculo del factor de compresibilidad Z:

def Z_factor(self, P):
    self.P = P
    self.Z = (self.P * self.V) / (self.nT * self.R * self.T)
    return self.Z

Calculo de la presión ideal del sistema:

def P_ideal(self, P):
    self.P = P
    self.Pxi = (self.ni * self.P) / self.nT
    return self.Pxi

Primera derivada parcial de la energía libre de Helmhotlz reducidad con respecto al volumen a temperatura y número de moles constantes:

def dF_dV(self):
    '''
    Primera derivada de F con respecto al volumen Ecu. (68)
    '''
    self.gv = self.R * self.B / (self.V * (self.V - self.B))
    self.fv = - 1 / ((self.V + self.s1 * self.B) * (self.V + self.s2 * self.B))
    self.ArV = -self.nT * self.gv * self.T - self.D * self.fv
    return self.ArV

Segunda derivada parcial de la energía libre de Helmhotlz reducidad con respecto al volumen a temperatura y número de moles constantes:

def dF_dVV(self):
    '''
    Segunda derivada de F con respecto al volumen Ecu. (74)
    '''
    self.gv2 = self.R * (1 / self.V ** 2 - 1 / (self.V - self.B) ** 2)
    self.fv2 = (- 1 / (self.V + self.s1 * self.B) ** 2 + 1 / (self.V + self.s2 * self.B) ** 2) / self.B / (self.s1 - self.s2)
    self.ArV2 = - self.nT * self.gv2 * self.T - self.D * self.fv2
    return self.ArV2

De esta formar se procede a determinar el valor del Volumen V para la presión P, temperatura T y número de moles N especificados para el sistema:

def volumen_1(self, P):
    '''
    Calculo del volumen V(T,P,n) del fluido a una temperatura T, presión P
    y número de moles totales nT especificados.
    Se utiliza el método de Newton con derivada de la función analitica.
    Pendiente cambiar por una función de Scipy.
    '''
    self.P = P
    self.V = 1.05 * self.B
    lnP = np.log(self.P)
    print "P_esp = ", self.P
    print "V_ini = ", self.V
    Pite = self.presion()
    lnPcal = np.log(Pite)
    #h = self.P - Pite
    h = lnP - lnPcal
    errorEq = abs(h)
    print "ErrorP = ", errorEq
    i = 0
    s = 1.0

    while errorEq > ep:
        self.parametro_D()
        self.parametro_B()
        self.dF_dV()
        self.dF_dVV()
        dPite = self.dP_dV()
        Pite = self.presion()
        lnPcal = np.log(Pite)
        #h = self.P - Pite
        h = lnP - lnPcal
        dh = -dPite
        #print self.nT
        self.V = self.V - s * h / dh
        errorEq = abs(h)
        #print "ErrorP = ", errorEq
        #print "V = ", self.V
        #print "Pite = ", Pite
        i += 1
        if i >= 900:
            pass
            #break
    print "FV = ", dPite

    return self.V

Para el cálculo de la función de la energía libre de Helmholtz que se muestra en la ecuación ( ), la cual escrita de esta forma es independiente del modelo termodinámico que se utilice ecuación de estado, además de facilitar la manipulación del sistema de ecauciones modelo de forma modular.

Función de la energía de Helmholtz

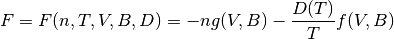
(15) $F = F (n,T,V,B,D) = -ng(V, B) - {D(T) \over T} f(V, B)$

Donde

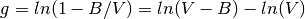
(16) $g = ln(1- B/V) = ln(V - B) - ln(V)$

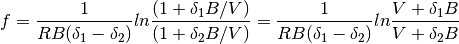
(17) $f = {1 \over RB(\delta_1 - \delta_2)} ln{(1 + \delta_1 B/V) \over (1 + \delta_2 B/V)} = {1 \over RB(\delta_1 - \delta_2)} ln{V + \delta_1 B \over V + \delta_2 B}$

Calculo de la función de energía F:

def funcion_energia_F(self):
    self.g = self.R * np.log(1 - self.B / self.V)
    self.bv = self.B / self.V
    self.f = np.log((self.V + self.s1 * self.B) / (self.V + self.s2 * self.B)) / self.B / (self.s1 - self.s2)
    self.Ar = -self.nT * self.g * self.T - self.D * self.f
    #print (("g = ", self.g))
    #print (("f: ", self.f))
    #print (("Ar: ", self.Ar))
    return self.g, self.f, self.Ar, self.bv

Elementos requeridos para calcular las primeras derivadas parciales de la función de energía de Helmholtz 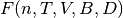$F(n,T,V,B,D)$

(18) $F_n = -g$

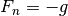
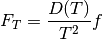
(19) $F_T = \frac{D(T)} {T^2} f$

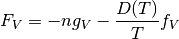
(20) $F_V = -ng_V - \frac{D(T)} {T} f_V$

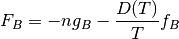
(21) $F_B = -ng_B - \frac{D(T)} {T} f_B$

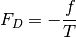
(22) $F_D = -\frac{f} {T}$

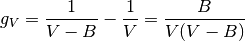
(23) $g_V = \frac{1} {V - B} - \frac{1}{V} = \frac{B}{V(V - B)}$

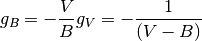
(24) $g_B = -\frac{V} {B} g_V = - \frac{1}{(V - B)}$

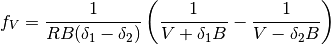
(25) $f_V = \frac{1} {RB(\delta_1 - \delta_2)} \left(\frac{1}{V + \delta_1B} - \frac{1}{V - \delta_2B}\right )$

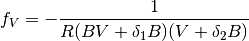
(26) $f_V = - \frac{1} {R(BV + \delta_1 B) (V + \delta_2B)}$

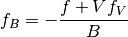
(27) $f_B = - \frac{f + Vf_V} {B}$

Primeras derivadas parciales de la función F de Helmhotlz con respecto al número de moles N para temperatura T y volumen V constantes, con respecto a la temperatura para V y N constantes y con respecto al volumen para T y N constantes, respectivamente.

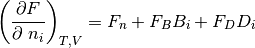
(28) $\left(\frac{\partial F} {\partial\ n_i}\right)_{T, V} = F_n + F_B B_i + F_D D_i$

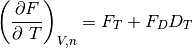
(29) $\left(\frac{\partial F} {\partial\ T}\right)_{V, n} = F_T + F_D D_T$

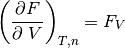
(30) $\left(\frac{\partial F} {\partial\ V}\right)_{T, n} = F_V$

Nota

En esl código se muestra solo para la primera derivadas parcial de la función F de Helmhotlz con respecto al número de moles N para temperatura T y volumen V constantes.

calculo de lprimeras derivadas:

def primeras_derivadas1(self):

    if nC == 1:
        AUX = self.R * self.T / (self.V - self.B)
        self.fB = -(self.f + self.V * self.fv) / self.B
        self.FFB = self.nT * AUX - self.D * self.fB
        self.Di = 2 * self.nT * self.ac * self.alfa
        self.Bi = self.bc
        self.Arn = -self.g * self.T + self.FFB * self.Bi - self.f * self.Di
    elif nC >= 2:
        # Derivando la ecuación (64) se obtiene la ecuación eq (106)
        self.Bi = np.ones((len(self.ni)))
        for i in range(nC):
            self.Bi[i] = (2 * self.aux[i] - self.B) / self.nT

        AUX = self.R * self.T / (self.V - self.B)
        self.fB = -(self.f + self.V * self.fv) / self.B
        self.FFB = self.nT * AUX - self.D * self.fB
        self.Arn = -self.g * self.T + self.FFB * self.Bi - self.f * self.Di

    print "Bi = ", self.Bi
    print "Di = ", self.Di
    print "fB = ", self.fB
    print "FFB = ", self.FFB
    print "Arn cal = ", self.Arn

    return self.Arn

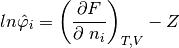
(31) $ln \hat\varphi_i = \left(\frac{\partial F} {\partial\ n_i}\right)_{T, V} - Z$

Una ve se ha obtenido la primera derivada parcial de la energía libre de Helmholtz, se puede calcular tanto la fugacidad como el coeficiente de fugacidad del sistema:

def coeficientes_fugacidad(self):
    self.Z = self.Z_factor(self.P)
    self.lnOi = self.Arn / (self.R * self.T) - np.log(self.Z)
    print "lnOi = ", self.lnOi
    self.Oi = np.exp(self.lnOi)
    print "Oi = ", self.Oi
    return self.Oi

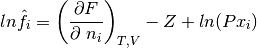
(32) $ln \hat f_i = \left(\frac{\partial F} {\partial\ n_i}\right)_{T, V} - Z + ln(Px_i)$

Calculo de la fugacidad:

def fugacidad(self):
    self.Z = self.Z_factor(self.P)
    self.Pxi = self.P_ideal(self.P)
    self.lnFi = self.Arn / (self.R * self.T) - np.log(self.Z) + np.log(self.Pxi)
    self.Fi = np.exp(self.lnFi)
    self.PHILOG = self.Arn / (self.R * self.T) - np.log(self.Z)

    print "Z = ", self.Z
    print "Arn = ", self.Arn
    print "lnFi = ", self.lnFi
    print "Fi = ", self.Fi
    print "PHILOG = ", self.PHILOG

    return self.Fi

En el método liquido se accede al cálculo de la fugacidad del fluido para los parametros y especificaciones determinadas. La fugacidad se guarda en la variable Fug que tiene la misma dimensión que el número de componentes nC del sistema:

def liquido(self, P):
    self.P = P
    ab = self.parametros(self.ni, self.nT, self.nC, self.V, self.T)
    print (("aij = ", ab[0]))
    print (("bij = ", ab[1]))
    print "................................................................"
    D = self.parametro_D()
    B = self.parametro_B()
    print (("D = ", D))
    print (("B = ", B))
    print "................................................................"
    Vol_1 = self.volumen_1(self.P)
    print (("Vol_1 = ", Vol_1))
    print (("Densidad =", 1 / Vol_1))
    print "................................................................"
    F = self.funcion_energia_F()
    print (("g = ", F[0]))
    print (("f = ", F[1]))
    print (("F = ", F[2]))
    print (("bv = ", F[3]))
    print "................................................................"
    dF = self.primeras_derivadas1()
    print (("dFdni = ", dF[0]))
    print (("dFdT = ", dF[1]))
    print (("dFdV = ", dF[2]))
    print "................................................................"
    Z = self.Z_factor(self.P)
    print "Z =", Z
    Zcal = (self.P * Vol_1) / (self.nT * self.R * self.T)
    print "Zcal =", Zcal
    print "................................................................"
    Pq = self.presion()
    print (("Pcal =", Pq))
    print "................................................................"
    Fug = self.fugacidad()
    #print (("Fug = ", Fug[0]))
    print (("Fug = ", Fug))
    print (("CoeFug = ", Fug / (self.ni * self.P)))
    print (("lnCoeFug = ", np.log(Fug / (self.ni * self.P))))
    print "................................................................"

    return Fug

A continuciṕon se muestra la forma en que se ingresan provisonalmente los parametros de inicialización para realizar los calculos. La inicialización corresponde a la especificación del número de componentes nC, la temperatura T en Kelvin, la presión P en Bar, la selección de la ecuación de estado eq y la tolerancia para determinar el Volumen V(P, T, N) del sistema:

#--------------------------- Númuro de componentes -----------------------------
#Número de componentes en el sistema
nC = 3
#---------------------------- Temperatura en K ---------------------------------
# K
T = 299.5
#-------------------------- Presión --------------------------------------------
# Bar
P = 1500.0
#--------------------------- Volumen ------------------------------------------
#--------------- Constante R [=] # bar.l/(mol.K) : 0.08314472-------------------
# bar.l/(mol.K) : 0.08314472
R = 0.08314472
#-------------------------------------------------------------------------------
#-------------------------------------------------------------------------------
# selección de la Ecuación de Estado
# eq = 1, para Ecuación de Estado (SRK)
# eq = 2, para Ecuación de Estado (PR)
eq = 2
#------------------ Criterio de convergencia en línea 215 ---------------------
#------------------ del método def volumen_1(self, P): ------------------------
ep = 1e-6
#------------------------------------------------------------------------------
#--------------------------- Fugacidad Fluido Puro ----------------------------
#------------------------------------------------------------------------------
print "..................................................................."

# metano - propano - C24
Tcm = np.array([190.56, 369.83, 804.0])
Pcm = np.array([45.99, 41.924, 9.672])
wm = np.array([0.0115, 0.1523, 1.071])

Nota

Los parametros de los modelos termodinámicos provisinalmente son escritos en el mismo archivo .py, mientras se integra un adminitrador de bases de datos.

Ahora se procede a instanciar la clase fluido = Helmholtz(eq, w, Tc, Pc, Tr, R) para luego acceder a los métodos parametros(ni, nT, nC, V, T) y liquido(P):

#---------------------------------------------------------------------------
# Tempertura reducidad
Tr = T / Tc

nT = np.sum(ni)
print "..................................................................."
fluido = Helmholtz(eq, w, Tc, Pc, Tr, R)
ab = fluido.parametros(ni, nT, nC, V, T)
print ab

flu_1 = fluido.liquido(P)

7.2 Resultados¶

Mientras se terminan los test para el código implmentado en Python para hacerlo de forma programatica, se hace una compración entre los resultados que se obtienen con las rutinas implementadas anteriormente en FORTRAN y los obtenidos en esta implmentación en la tabla (1) para un componente puro y en la talba (2) para una mezcla.

Tabla 1. Comparación de resultados entre IPyTherm y GPEC, Macla 1

P = 200.0 Bar T = 368.0 K 1 mol C1
Variable	PyTherm	GPEC
V	0.14160332	0.141604834257319
g	-0.01744569	-0.01744577009114121
f	6.04150003	6.04143211028481
fB	-29.17898803	-29.1783074191090
FFB	318.78279781	318.778307258157
Arn	-6.67700465	-6.67643301466508
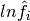$ln \hat f_i$	5.15741367	5.15742167555949

Tabla 2. Comparación de resultados entre IPyTherm y GPEC, Mezcla 2

P = 800.0 Bar T = 368.0 K
C1 = 0.30 moles, C24 = 0.70 moles
Variable	PyTherm \| GPEC
Arn
C1	79.86005173	79.86079
C24	-73.51719121	-73.51722
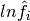$ln \hat f_i$
C1	5.74717729	5.74720
C24	1.5816976	1.58170

Tabla 3. Comparación de resultados entre IPyTherm y GPEC, Mezcla 3

P = 800.0 Bar T = 368.0 K
C1 = 0.8224 moles, C3 = 0.0859 moles, C24 = 0.0917 moles
Variable	PyTher	GPEC
V	0.097895788494793759	0.09712098988665994
g	-0.12547030006562548	-0.125067142383822
f	6.7115641252706366	6.76716180547646
fB	-19.3589126132	-19.7063420668040
FFB	1635.57161009	1641.91328887125
Ar	-30.818627700503917	-30.9082104588285
Arn
C1	31.03421463	31.0357268368683
C2	-6.35640646	-6.35637488487487
C24	-95.8172984	-95.8172808890964
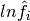$ln \hat f_i$
C1	6.7671523	6.76703848796874
C2	5.5448668	5.54496483049592
C24	2.6217857	2.62114371407445

7.3 Conclusiones¶

Se implemento en el lenguaje de programación Python el cálculo de la fugacidad de fluidos puros y mezclas multicomponente siguiendo el enfoque modular de la función de la energía de Helmholtz con ecuaciones de estado (SRK) (PR) con las reglas de mezclado (VDW).

Al comparar los resultados obtenidos con IPyTherm 1.0 y GPEC, se encuentran concordancia numérica para las variables de los casos de revisión planteados, excepto para el valor de la fugacidad de los componentes de la mezcla 3.

Nota

La diferencia que existe entre el valor de la fugacidad de la mezcla 3 al comparar con los datos de GPEC, puede ser debida a errores de transcripción. Pendiente por confirmar.

Este modulo enfocado en el calculo de la fugacidad de fluidos puros y mezclas multicomponente, puede ser integrado para realizar cálculos de fugacidad en sólidos.

7.4 Referencias¶

[1]	Michael L. Michelsen and Jorgen M. Mollerup. Thermodynamics Models: Fundamentals & Computacional aspects. Denmark. Second Edition. 2007.

[2]	Python web: https://www.python.org/

[3]	Sphinx web: http://sphinx-doc.org/

[4]	Jupyter web: https://jupyter.org/