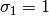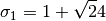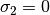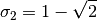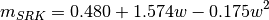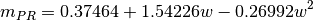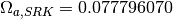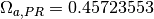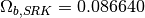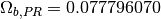6. Cálculo del Volumen(P,T,n)¶

6.1 Introduction¶

En esta sección se presenta un ejemplo numérico para calcular propiedades termodinámicas y volumetricas utilizando ecuaciones de estado. Para comenzar se desarrolla el procedimiento que permite determinar el volumen de un sistema cuando se especifica la presión P, la temperatura T y el número de moles n, cuya interdependencia entre estás variables es como se muestra en la ecuación (1)

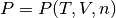
(1) $P = P(T,V,n)$

La ecuación de presión tradicionalmente se conoce como una ecuación de estado explicita en el termino de la presión, la cual se relaciona con la función residual de Helmholtz 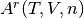$A^r(T,V,n)$ que es una función que depende de las variables de estado de una mezcla 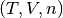$(T,V,n)$ menos el equivalente de las mismas variables de estado como una mezcla 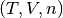$(T,V,n)$ de gas ideal, tal como se muestra a continuación en la ecuación (2)

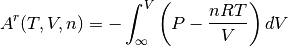
(2) $A^r(T,V,n) = -\int_\infty^{V} \left(P - \frac{nRT} {V}\right) dV$

y recordando la relación simple del número de moles de la mezcla multicomponente en la ecuación (3)

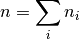
(3) $n = \sum\limits_{i} {n_i}$

Al reorganizar la ecuación (2), se obtiene la tradicional ecuación de estado explicita en la presión como una contribución del negativo de la derivada parcial de la función de Helmohtlz con respecto al volumen V, la temperatura T y número de moles n constante, más el termino de la ecuación de gas ideal, tal como se muestra en la ecuación (4).

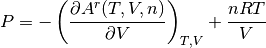
(4) $P = - \left(\frac{\partial A^r(T,V,n)} {\partial V}\right)_{T, V} + \frac {nRT}{V}$

definiciendo la variable F como la función de Herlmhotlz residual redicida, como en la ecuación (5)

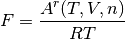
(5) $F = \frac{A^r(T,V,n)} {RT}$

se obtiene una función de Helmohtlz residual reducida cuya funcionalidad es como se muestra en la ecuación (6)

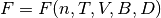
(6) $F = F(n,T,V,B,D)$

es decir, que de esta forma, la ecuación de estado explicita en la presión del sistema se puede reescribir como en la ecuación (7)

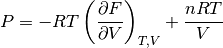
(7) $P = - RT \left(\frac{\partial F} {\partial V}\right)_{T, V} + \frac {nRT}{V}$

ahora es posible obtener las expresiones de las derivadas parciales de la presión con respecto a cada una de las variables del sistema

Derivada parcial de la presión P con respecto al volumen V, ecuación (8)

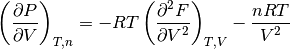
(8) $\left(\frac{\partial P}{\partial V}\right)_{T,n} = - RT \left(\frac{\partial^2 F} {\partial V^2}\right)_{T, V} - \frac {nRT}{V^2}$

Derivada parcial de la presión P* con respecto a la temperatura T, ecuación (9)

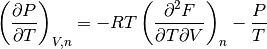
(9) $\left(\frac{\partial P}{\partial T}\right)_{V,n} = - RT \left(\frac{\partial^2 F} {\partial T \partial V}\right)_{n} - \frac {P}{T}$

Derivada parcial de la presión P* con respecto al número de moles de cada componente 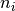$n_i$ , ecuación (10)

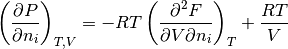
(10) $\left(\frac{\partial P}{\partial n_i}\right)_{T,V} = - RT \left(\frac{\partial^2 F} {\partial V \partial n_i}\right)_{T} + \frac {RT}{V}$

Derivada parcial del volumen V con respecto al número de moles de cada componente $n_i$ , ecución (11)

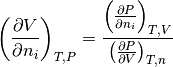
(11) $\left(\frac {\partial V}{\partial n_i}\right)_{T,P} = \frac {\left(\frac{\partial P} {\partial n_i}\right)_{T,V}} {\left(\frac {\partial P}{\partial V} \right)_{T,n}}$

6.2 Método de Solución¶

Luego de presentar las ecuaciones necesarias en la sección 4.1, ahora se formula la función objetivo con la cual se implementa un método numérico para encońtran los ceros de una función no lineal, por tanto al especificar la presión 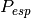$P_{esp}$ , temperatura T y número de moles del sistema n, se quiere encontrar el volumen de la mezcla que cumpla con un valor de la presión determinado usando una ecuación de estado 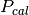$P_{cal}$ . De esta forma, se plantea la función objetivo 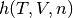$h(T,V,n)$ que se muestra en la ecuación (12)

Función objetivo que se formula para este caso:

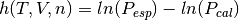
(12) $h(T,V,n) = ln(P_{esp}) - ln(P_{cal})$

y su primera derivada analítica, se muestra en la ecuación (13)

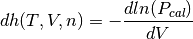
(13) $dh(T,V,n) = -\frac {dln(P_{cal})}{dV}$

por tanto, para efectos didacticos se implementa el método de Newton en una sola variable, en este caso para determinar el Volumen V, tal como se muestra en la ecuación (14)

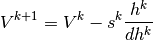
(14) $V^{k+1} = V^k - s^k \frac {h^k} {dh^k}$

por defecto el parametro es s tiene un valor de la unidad, 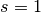$s = 1$

y la ecuación (12), es resuelta con una tolerancia de error como se muestra en la ecuación (15)

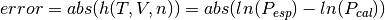
(15) $error = abs(h(T,V,n)) = abs(ln(P_{esp}) - ln(P_{cal}))$

como ya se había mencionado anteriormente, la presión del sistema está dada por la suma de dos terminos, el primero corresponde a la función de Helmhotlz y el segundo a la parte de la ecuación de gas idea.

Nota

El cálculo de la función de Helmholtz que se muestra a continuación, escrita de la forma que tiene la ecuación (16), es independiente del modelo termodinámico que se utilice: ecuación de estado, además de permitir la manipulación modular del sistema de ecauciones.

Función de la energía de Helmholtz

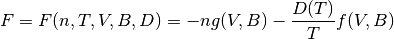
(16) $F = F (n,T,V,B,D) = -ng(V, B) - {D(T) \over T} f(V, B)$

Donde los terminos (g) y (f)de la ecuación (16), se muestran en las ecuaciones (17) y (18), respectivamente

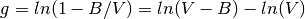
(17) $g = ln(1- B/V) = ln(V - B) - ln(V)$

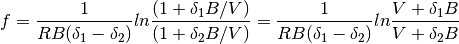
(18) $f = {1 \over RB(\delta_1 - \delta_2)} ln{(1 + \delta_1 B/V) \over (1 + \delta_2 B/V)} = {1 \over RB(\delta_1 - \delta_2)} ln{V + \delta_1 B \over V + \delta_2 B}$

6.3 Derivadas Parciales¶

Anteriormente se comentó, el enfoque modular de Michelsen & Mollerup permite estructurar los diferentes elementos necesarios para el cálculo de propiedades termidinámicas en forma de bloques, por tanto se presenta la forma modular que resultan para las primeras y segundas derivadas parciales de la función de la energía de Helmholtz. Al iniciar, se presenta en la ecuación (19) la primera derivada parcial de la función F

Primera derivada parcial de F con respecto al volumen V, con T y n constantes

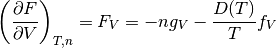
(19) $\left( \frac {\partial F}{\partial V} \right)_{T,n} = F_{V} = -ng_V - \frac{D(T)} {T} f_V$

de igual forma, en los terminos :math: g_V y :math: f_V, se muestran en las ecuaciones (20) y (21), respectivamente

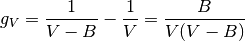
(20) $g_V = \frac{1} {V - B} - \frac{1}{V} = \frac{B}{V(V - B)}$

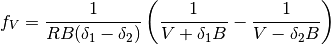
(21) $f_V = \frac{1} {RB(\delta_1 - \delta_2)} \left(\frac{1}{V + \delta_1B} - \frac{1}{V - \delta_2B}\right )$

la ecuación (21) tiene una forma alternativa más compacta como la que se muestra en la ecuación (22)

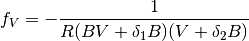
(22) $f_V = - \frac{1} {R(BV + \delta_1 B) (V + \delta_2B)}$

siguiendo el mismo procedimiento, se obtiene la segunda derivada parcial de la función F con respecto al volumen y esta, se muestra en la ecuación (23)

Segunda derivada parcial de F con respecto al volumen V, con T y n constantes

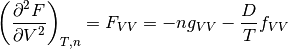
(23) $\left( \frac {\partial^2 F}{\partial V^2} \right)_{T,n} = F_{VV} = -ng_{VV} - \frac{D}{T}f_{VV}$

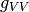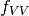como en el caso anterior, en los terminos $g_{VV}$ y $f_{VV}$ , se muestran en las ecuaciones (24) y (25), respectivamente

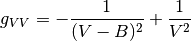
(24) $g_{VV} = -\frac {1}{(V-B)^2} + \frac{1}{V^2}$

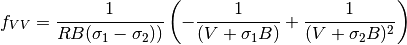
(25) $f_{VV} = \frac{1}{RB(\sigma_1-\sigma_2))} \left(- \frac{1}{(V+\sigma_1 B)} + \frac{1}{(V+\sigma_2B)²}\right)$

En las ecuaciones anteriores de la función, primera derivada y segunda derivada de Helmhotlz aparecen los parametros D y B que se expresan como se muestran en las ecuaciones (26) y (28), respectivamente

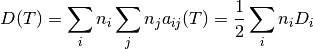
(26) $D(T) = \sum\limits_{i} {n_i \sum\limits_{j} {n_ja_{ij}(T)} = {1\over 2} \sum\limits_{i} {n_i D_i} }$

donde 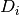$D_i$ es la derivada de 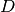$D$ con respecto al número de moles 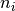$n_i$ de la mezcla, que tiene la forma de la ecuación (27)

Primera derivada parciale del parámetro 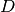$D$ con respecto a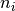 $n_i$

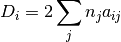
(27) $D_i = 2 \sum\limits_{j} {n_ja_{ij}}$

en el caso del parámetro B, la ecuación (28) presenta la forma de realizar su cálculo

Parametro B

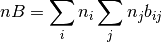
(28) $nB = \sum\limits_{i} {n_i \sum\limits_{j} {n_jb_{ij}}}$

Para el caso de un componente puro en el sistema, el parametro B (lij = 0) se calcula como se muestra en la ecuación (29)

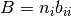
(29) $B = n_i b_{ii}$

y para el caso de una mezcla, la ecuación (29) se reescribe en la orma de la ecuación (30)

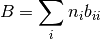
(30) $B = \sum\limits_{i} n_i b_{ii}$

Las derivadas parciales del parametro B con respecto al número de moles ni, se obtiene al resolver las ecuaciones (31) y (32)

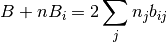
(31) $B + nB_i = 2 \sum\limits_{j} {n_jb_{ij}}$

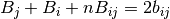
(32) $B_j + B_i + nB_{ij} = 2b_{ij}$

Resolviendo el sistema de las ecuaciones (31) y (32), se obtiene las ecuaciones (33) y (34)

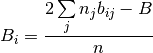
(33) $B_i = \frac{2 \sum\limits_{j} {n_jb_{ij} - B} } {n}$

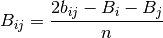
(34) $B_{ij} = \frac{2 b_{ij} - B_i - B_j} {n}$

De esta manera, ya se cuenta con las ecuaciones necesarias para obtener las primeras y segundas derivadas de la función F con respecto al V a P, T y ni constantes.

6.4 Ecuación de estado¶

Hasta acá se ha presentado la manipulaciṕon básica de la función de Herlmhotlz que partiendo de una expresión explicita en la presión como una ecuación de estado, el sistema de ecuaciones se pueda resolver una vez se especificá la presión P, la temperatura T y número de moles n y proceder a la determinación del valor del volumen V correspondiente para un modelo termmodinámico y componentes prestablecidos.

Para este caso se utiliza el modelo de: Ecuación de estado cúbica, cuya forma básica se muestra en la ecuación (35)

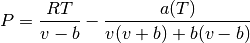
(35) $P = \frac{RT}{v-b} - \frac{a(T)}{v(v+b)+b(v-b)}$

en la cual, se requieren los parámetros que se presentan en las ecuaciones (36)-(39)

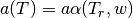
(36) $a(T) = a \alpha(T_r,w)$

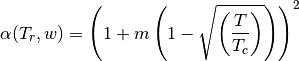
(37) $\alpha(T_r,w) = \left(1 + m\left(1 - \sqrt{\left(\frac{T} {T_c}\right)}\right) \right)^2$

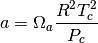
(38) $a = \Omega_{a} \frac{R^2T_c^2} {P_c}$

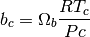
(39) $b_c = \Omega_{b} \frac {R T_c} {Pc}$

estos parámetros, se relacionan con los valores caracteristicos para los modelos Soave-Redlich-Kwong (SRK) y Peng-Robinson (PR), en las ecuaciones ()-()

Tabla 1. Parámetros de ecuaciones de estado utilizadas

Soave-Redlich-Kwong		Peng-Robinson
$\sigma_1 = 1$		$\sigma_1 = 1+\sqrt{2}4$
$\sigma_2 = 0$		$\sigma_2 = 1-\sqrt{2}$
$m_{SRK} = 0.480 + 1.574w - 0.175w^2$		$m_{PR} = 0.37464 + 1.54226w - 0.26992w^2$
$\Omega_{a,SRK} = 0.077796070$		$\Omega_{a,PR} = 0.45723553$
$\Omega_{b,SRK} = 0.086640$		$\Omega_{b,PR} = 0.077796070$

6.5 Resultados¶

A continuación se presenta un ejemplo numérico del cálculo del volumen de una mezcla multicomponente con las especificaciones de presión P, temperatura T y número de moles n, que se muestran en la Tabla 2.

Tabla 2. Comparación de resultados entre PyTher y GPEC

P = 800.0 Bar T = 368.0 K
C1 = 0.8224 moles, C3 = 0.0859 moles, C24 = 0.0917 moles
Variable	PyTherm	GPEC
V	0.097188024166321052	0.09712098988665994

En la tabla 2, se puede observar que para el ejemplo presentado en este documento el procedimiento implementado en Python se puede considerar validado.

Nota

Se requiere probar el código implementado con más casos que involucren un mayor número de componentes, tipos de componentes y otras especificaciones de presión, temperatura y número de moles.

4.6 Conclusiones¶

Se presentó el procedimiento básico para calcular el volumen de una mezcla multicomponente usando el enfoque modular de Michelsen & Mollerup con las ecuaciones de estado SRK y PR.
Se implmento el algoritmo para el cálculo del volumen en el lenguaje de programación Python en la plataforma Jupyter.

6.7 Referencias¶

[1]	Michael L. Michelsen and Jorgen M. Mollerup. Thermodynamics Models: Fundamentals & Computacional aspects. Denmark. Second Edition. 2007.

[2]	Python web: https://www.python.org/

[3]	Sphinx web: http://sphinx-doc.org/

[4]	Jupyter web: https://jupyter.org/